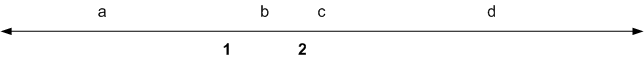Today sees local elections across the UK, with the highest profile battle being fought over the mayorship of London. While there are two high-profile candidates in Boris Johnson and Ken Livingstone, there are a number of other candidates who represent a whole range of political views from the far right to the far left.
There is a significant third candidate in the middle, Brian Paddick. While he is unlikely to get elected, he has a significant impact on the policies of the two front-runners. There are many differences in policies between the Conservatives and Labour, and this difference is driven by the existence of the third option.
This can be compared to the situation with elections in the US. In many cases, policies between the two main parties are almost identical, and this is caused by the lack of a viable alternative to these candidates. This type of convergence derives from the need for political parties to appeal to voters.
Consider a simplified political landscape, with a single spectrum of policies. There are two potential candidates, 1 and 2, and four voters. These four voters are spread across the spectrum as shown below.
As it stands, it is clear that a will vote for 1, and d will vote for 2. This is not to say that these voters completely agree with the policies of their chosen candidate – indeed, we can see that a believes that 1 is a bit too “right” for them, while d considers 2 too “left”. However, these candidates are the closest to the ideal.
What about the remaining two candidates? b is likely to vote for 1, since although 1 is a little too “left” it is the nearest to the ideal. c is midway between the two candidates and so could be convinced either way. In any case, 2 will not win this election; the best they can hope for is a tie.
It is easy to conclude that all voters to the left of 1 will vote for 1, and all voters to the right of 2 will vote for 2. The election will be decided by the treatment of voters in the middle of the two candidates. By moving along the political spectrum, 2 will be able to capture some of these middle voters, as shown below.
d will still vote for 2, since they represent the best option, even if they are further away from d’s ideals. c will now definitely vote for 2, since they are closer to 2 than they are to 1. By moving closer to 1’s position, 2 has won the election. This analysis can be iterated; 1 may move closer to 2 in order to guarantee b’s vote and force a tie.
In general cases, there are more than four voters and there is a continuum of preferences; due to this, 1 and 2 will move closer and closer to each other until there is little difference between the two. 1 and 2 will end up both positioned in the middle of the spectrum, with equal numbers of voters on each side.
However, entering a third candidate onto this spectrum disrupts the convergence. A third candidate could position themselves to capture both c and d, and 2 would instead move back along the spectrum to recapture lost voters. There is in fact no steady state equilibrium to this situation; any move by any player immediately changes the best response by others. In the UK it can be seen that political parties are constantly moving along the spectrum, with (for example) Tony Blair’s “New Labour” being a more right-wing relaunch of the Labour party.
The situation is made more complex by the fact that there is more than one spectrum to be considered: voters consider how a party will deal with policing, with healthcare, with liberties, with the economy. Rather than examining candidates on a single line, voters will instead carry out some sort of multidimensional nearest neighbour analysis. As long as there are at least two more candidates than there are dimensions, voters will be left with a choice of policies, rather than being dictated by political parties meeting in the middle.